8.5 Computing Moments from Samples

Given a Lie group $G$ (with algebra $\mathfrak{g}$) and a set of $N$ samples $x_{i}\in G$, we can estimate the mean and covariance iteratively. First, any of the samples provides an initial guess for the mean:

$$\mu_{0}\leftarrow x_{0}$$ (229)

Then, new estimates of the mean and covariance can be computed in terms of deviations in the tangent space:

$$v_{i,k} \equiv \ln\left(x_{i}\cdot\mu_{k}^{-1}\right)$$ (230)

$$\boldsymbol{\Sigma}_{k} \leftarrow \dfrac{1}{N}\sum_{i}\left[v_{i,k}\cdot v_{i,k}^{T}\right]$$ (231)

$$\mu_{k+1} \leftarrow \exp\left(\dfrac{1}{N}\sum_{i}v_{i,k}\right)\cdot\mu_{k}$$ (232)

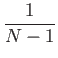Iterating these updates should rapidly converge (typically in two or three iterations). Replacing the factor $\dfrac{1}{N}$ with $\dfrac{1}{N-1}$ in Eq. 231 yields an unbiased estimate of the covariance.