4.2 Exponential Map

The exponential map that takes skew symmetric matrices to rotation matrices is simply the matrix exponential over a linear combination of the generators:

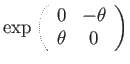$$\exp\left(\theta_{\times}\right) \equiv \exp\left(\begin{array}{cc} 0 & -\theta\\ \theta & 0 \end{array}\right)$$ (95)

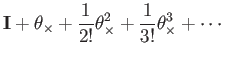$$= \mathbf{I}+\theta_{\times}+\frac{1}{2!}\theta_{\times}^{2}+\frac{1}{3!}\theta_{\times}^{3}+\cdots$$ (96)

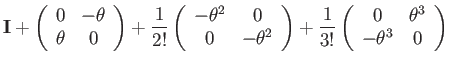$$= \mathbf{I}+\left(\begin{array}{cc} 0 & -\theta\\ \theta & 0 \end... ...3!}\left(\begin{array}{cc} 0 & \theta^{3}\\ -\theta^{3} & 0 \end{array}\right)$$ (97)

The resulting elements form the Taylor series expansion of $\sin\theta$ and $\cos\theta$:

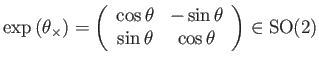$$\exp\left(\theta_{\times}\right)=\left(\begin{array}{cc} \cos\theta & -\sin\theta\\ \sin\theta & \cos\theta \end{array}\right)\in\mathrm{SO(2)}$$ (98)

Thus the exponential map yields a rotation by $\theta$ radians.

The exponential map can be inverted, going from $\mathrm{SO}(2)$ to $\mathrm{so}(2)$:

$$\mathbf{R} \in \mathrm{SO}(2)$$ (99)

$$\ln\left(\mathbf{R}\right)=\theta = \arctan\left(\mathbf{R}_{21},\mathbf{R}_{11}\right)$$ (100)