5.1 Representation

The group of rigid transformations in 2D space, $\mathrm{SE}(2)$ , is represented by linear transformations on homogeneous three-vectors:

$\displaystyle \mathbf{R}$	$\displaystyle \in$	$\displaystyle \mathrm{SO}(2),\:\mathbf{t}\in\mathbb{R}^{2}$	(101)
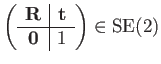$\displaystyle C$	$\displaystyle =$	$\displaystyle \left(\begin{array}{c\vert c} \mathbf{R} & \mathbf{t}\\ \hline \mathbf{0} & 1 \end{array}\right)\in\mathrm{SE}(2)$	(102)

Note that, in an implementation, only $\mathbf{R}$ and $\mathbf{t}$ need to be stored. The remaining matrix structure can remain implicit.

Transformation composition and inversion are coincident with matrix multiplication and inversion:

$\displaystyle C_{1},C_{2}$	$\displaystyle \in$	$\displaystyle \mathrm{SE}(2)$	(103)
$\displaystyle C_{1}\cdot C_{2}$	$\displaystyle =$	$\displaystyle \left(\begin{array}{c\vert c} \mathbf{R}_{1} & \mathbf{t}_{1}\\ ... ... c} \mathbf{R}_{2} & \mathbf{t}_{2}\\ \hline \mathbf{0} & 1 \end{array}\right)$	(104)
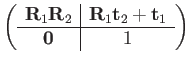	$\displaystyle =$	$\displaystyle \left(\begin{array}{c\vert c} \mathbf{R}_{1}\mathbf{R}_{2} & \mat... ...R}_{1}\mathbf{t}_{2}+\mathbf{t}_{1}\\ \hline \mathbf{0} & 1 \end{array}\right)$	(105)
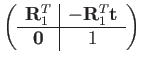$\displaystyle C_{1}^{-1}$	$\displaystyle =$	$\displaystyle \left(\begin{array}{c\vert c} \mathbf{R}_{1}^{T} & -\mathbf{R}_{1}^{T}\mathbf{t}\\ \hline \mathbf{0} & 1 \end{array}\right)$	(106)

The matrix representation also makes the group action on 2D points and vectors explicit:

$\displaystyle \mathbf{x}$	$\displaystyle =$	$\displaystyle \left(\begin{array}{ccc} x & y & w\end{array}\right)^{T}\in\mathbb{RP}^{2}\quad(\lambda\mathbf{x}\simeq\mathbf{x}\:\forall\lambda\in\mathbb{R})$
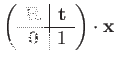$\displaystyle C\cdot\mathbf{x}$	$\displaystyle =$	$\displaystyle \left(\begin{array}{c\vert c} \mathbf{R} & \mathbf{t}\\ \hline \mathbf{0} & 1 \end{array}\right)\cdot\mathbf{x}$	(107)
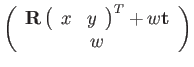	$\displaystyle =$	$\displaystyle \left(\begin{array}{c} \mathbf{R}\left(\begin{array}{cc} x & y\end{array}\right)^{T}+w\mathbf{t}\\ w \end{array}\right)$	(108)

Typically,

, so that $\mathbf{x}$ is a Cartesian point. The action by matrix-vector multiplication corresponds to first rotating $\mathbf{x}$ and then translating it. For direction vectors, encoded with

translation is ignored.

The Lie algebra $\mathrm{se}(2)$ is the set of $3\times3$ matrices corresponding to differential translations and rotation around the identity. There are thus three generators of the algebra:

$\begin{displaymath}\begin{array}{ccc} G_{1}=\left(\begin{array}{ccc} 0 & 0 & 1\\... ... & -1 & 0\\ 1 & 0 & 0\\ 0 & 0 & 0 \end{array}\right)\end{array}\end{displaymath}$

(109)

An element of $\mathrm{se}(2)$ is then represented by linear combinations of the generators:

$\displaystyle \left(\begin{array}{ccc} \mathbf{u}_{1} & \mathbf{u}_{2} & \theta\end{array}\right)^{T}$	$\displaystyle \in$	$\displaystyle \mathbb{R}^{3}$	(110)
$\displaystyle \mathbf{u}_{1}G_{1}+\mathbf{u}_{2}G_{2}+\theta G_{3}$	$\displaystyle \in$	$\displaystyle \mathrm{se}(2)$	(111)

For convenience, we write $\left(\begin{array}{cc} \mathbf{u} & \theta\end{array}\right)^{T}\in\mathrm{se}(2)$ , with multiplication against the generators implied.