5.2 Exponential Map

As for all Lie groups in this document, the exponential map from $\mathrm{se}(2)$ to $\mathrm{SE}(2)$ is the matrix exponential on a linear combination of the generators:

$\displaystyle \boldsymbol{\delta}=\left(\begin{array}{cc} \mathbf{u} & \theta\end{array}\right)$	$\displaystyle \in$	$\displaystyle \mathrm{se}(2)$	(112)
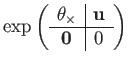$\displaystyle \exp\left(\boldsymbol{\delta}\right)$	$\displaystyle =$	$\displaystyle \exp\left(\begin{array}{c\vert c} \theta_{\times} & \mathbf{u}\\ \hline \mathbf{0} & 0 \end{array}\right)$	(113)
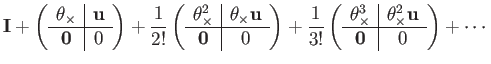	$\displaystyle =$	$\displaystyle \mathbf{I}+\left(\begin{array}{c\vert c} \theta_{\times} & \mathb... ...theta_{\times}^{2}\mathbf{u}\\ \hline \mathbf{0} & 0 \end{array}\right)+\cdots$	(114)

The rotation block is the same as for $\mathrm{SO}(2)$ , but the translation component is a different power series:

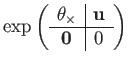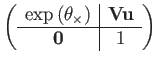$\displaystyle \exp\left(\begin{array}{c\vert c} \theta_{\times} & \mathbf{u}\\ \hline \mathbf{0} & 0 \end{array}\right)$	$\displaystyle =$	$\displaystyle \left(\begin{array}{c\vert c} \exp\left(\theta_{\times}\right) & \mathbf{V}\mathbf{u}\\ \hline \mathbf{0} & 1 \end{array}\right)$	(115)
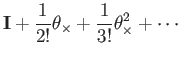$\displaystyle \mathbf{V}$	$\displaystyle =$	$\displaystyle \mathbf{I}+\frac{1}{2!}\theta_{\times}+\frac{1}{3!}\theta_{\times}^{2}+\cdots$	(116)

$\displaystyle \mathbf{V}$

$\displaystyle =$

$\displaystyle \sum_{i=0}^{\infty}\left[\dfrac{\theta_{\times}^{2i}}{(2i+1)!}+\dfrac{\theta_{\times}^{2i+1}}{(2i+2)!}\right]$

(117)

Two identities (easily confirmed by induction) are useful for collapsing the series:

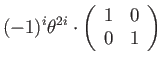$\displaystyle \theta_{\times}^{2i}$	$\displaystyle =$	$\displaystyle (-1)^{i}\theta^{2i}\cdot\left(\begin{array}{cc} 1 & 0\\ 0 & 1 \end{array}\right)$	(118)
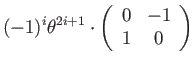$\displaystyle \theta_{\times}^{2i+1}$	$\displaystyle =$	$\displaystyle (-1)^{i}\theta^{2i+1}\cdot\left(\begin{array}{cc} 0 & -1\\ 1 & 0 \end{array}\right)$	(119)

Direct application of the identies yields a reduced expression for $\mathbf{V}$ in terms of diagonal and skew-symmetric components:

$\displaystyle \mathbf{V}$	$\displaystyle =$	$\displaystyle \sum_{i=0}^{\infty}(-1)^{i}\theta^{2i}\left[\dfrac{1}{(2i+1)!}\cd... ...{(2i+2)!}\cdot\left(\begin{array}{cc} 0 & -1\\ 1 & 0 \end{array}\right)\right]$	(120)
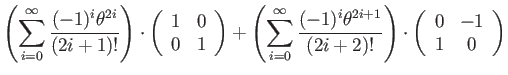	$\displaystyle =$	$\displaystyle \left(\sum_{i=0}^{\infty}\dfrac{(-1)^{i}\theta^{2i}}{(2i+1)!}\rig... ...{(2i+2)!}\right)\cdot\left(\begin{array}{cc} 0 & -1\\ 1 & 0 \end{array}\right)$	(121)

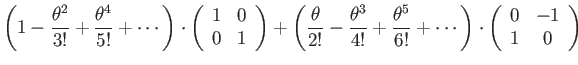$\displaystyle \mathbf{V}$	$\displaystyle =$	$\displaystyle \left(1-\frac{\theta^{2}}{3!}+\frac{\theta^{4}}{5!}+\cdots\right)... ...!}+\cdots\right)\cdot\left(\begin{array}{cc} 0 & -1\\ 1 & 0 \end{array}\right)$	(122)
	$\displaystyle =$	$\displaystyle \left(\dfrac{\sin\theta}{\theta}\right)\cdot\left(\begin{array}{c... ...}{\theta}\right)\cdot\left(\begin{array}{cc} 0 & -1\\ 1 & 0 \end{array}\right)$	(123)
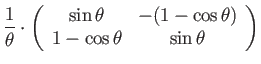	$\displaystyle =$	$\displaystyle \dfrac{1}{\theta}\cdot\left(\begin{array}{cc} \sin\theta & -(1-\cos\theta)\\ 1-\cos\theta & \sin\theta \end{array}\right)$	(124)

For implementation purposes, Taylor expansions should be used for $\mathbf{V}$ when $\theta$ is small.

The $\ln()$ function on $\mathrm{SE}(2)$ can be implemented by first recovering $\theta=\ln(\mathbf{R})$ as shown in Eq. 100, then solving $\mathbf{Vu}=\mathbf{t}$ for $\mathbf{u}$ in closed form:

$\displaystyle A$	$\displaystyle \equiv$	$\displaystyle \dfrac{\sin\theta}{\theta}$	(125)
$\displaystyle B$	$\displaystyle \equiv$	$\displaystyle \dfrac{1-\cos\theta}{\theta}$	(126)
$\displaystyle \mathbf{V}^{-1}$	$\displaystyle =$	$\displaystyle \dfrac{1}{A^{2}+B^{2}}\left(\begin{array}{cc} A & B\\ -B & A \end{array}\right)$	(127)
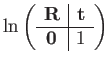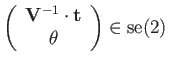$\displaystyle \ln\left(\begin{array}{c\vert c} \mathbf{R} & \mathbf{t}\\ \hline \mathbf{0} & 1 \end{array}\right)$	$\displaystyle =$	$\displaystyle \left(\begin{array}{c} \mathbf{V}^{-1}\cdot\mathbf{t}\\ \theta \end{array}\right)\in\mathrm{se(2)}$	(128)