Next: 4 SO(2): Rotations in Up: 3 SE(3): Rigid transformations Previous: 3.3 Adjoint
Consider
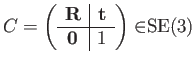 and
and
![]() . The transformation of vector
. The transformation of vector
![]() by C is given by multiplication:
by C is given by multiplication:
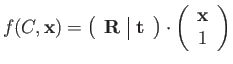 |
(83) | ||
| (84) |
Then differentiation by the vector is straightforward, as ![]() is
linear in
is
linear in
![]() :
:
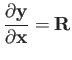 |
(85) |
Just as with
![]() , differentiation by the transformation
parameters is performed by left multiplying the product by the generators
(here with their last rows removed):
, differentiation by the transformation
parameters is performed by left multiplying the product by the generators
(here with their last rows removed):
| (86) |
Again, differentiation of a product of transformations is trivial given the adjoint:
| (87) | |||
![$\displaystyle \dfrac{\partial}{\partial\mathbf{\boldsymbol{\delta}}}\left[C_{1}\cdot\exp\left(\mathbf{\boldsymbol{\delta}}\right)\cdot C_{0}\right]$](img185.png) |
(88) | ||
| (89) |
Ethan Eade 2012-02-16