Next: 3.4 Jacobians Up: 3 SE(3): Rigid transformations Previous: 3.2 Exponential Map
The adjoint in
![]() is computed from the generators,
just as in
is computed from the generators,
just as in
![]() :
:
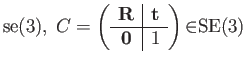 |
(78) | ||
| (79) | |||
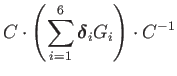 |
(80) | ||
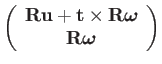 |
(81) | ||
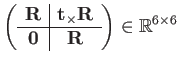 |
(82) |
Note that moving a tangent vector via the adjoint mixes the rotation component into the translation component.