Next: 6.2 Exponential Map Up: 6 Sim(3): Similarity Transformations Previous: 6 Sim(3): Similarity Transformations
Similarity transformations are combinations of rigid transformation
and scaling. The group of similarity transforms in 3D space,
![]() ,
has a nearly identical representation to
,
has a nearly identical representation to
![]() ), with an
additional scale factor:
), with an
additional scale factor:
| (133) | |||
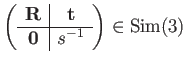 |
(134) |
Again, group operations map are isomorphic with matrix operations:
| (135) | |||
 |
(136) | ||
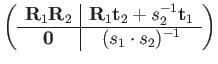 |
(137) | ||
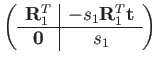 |
(138) |
The group action on 3D points also encodes scaling by ![]() :
:
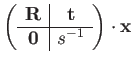 |
(139) | ||
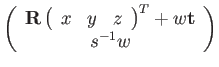 |
(140) | ||
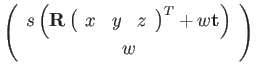 |
(141) |
In the typical case with ![]() , this corresponds to rigid transformation
followed by scaling.
, this corresponds to rigid transformation
followed by scaling.
The generators of the Lie algebra
![]() are identical
to those of
are identical
to those of
![]() (Eq. 58), with the addition
of a generator corresponding to scale change:
(Eq. 58), with the addition
of a generator corresponding to scale change:
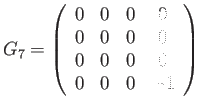 |
(142) |
An element of
![]() is represented by multiples of the
generators:
is represented by multiples of the
generators:
| (143) | |||
| (144) |
For convenience, we write
![]() , with multiplication against the generators implied.
, with multiplication against the generators implied.
Ethan Eade 2012-02-16