Next: 6.3 Adjoint Up: 6 Sim(3): Similarity Transformations Previous: 6.1 Representation
As above, the exponential map from
![]() to
to
![]() is the matrix exponential on a linear combination of the generators:
is the matrix exponential on a linear combination of the generators:
| (145) | |||
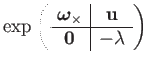 |
(146) | ||
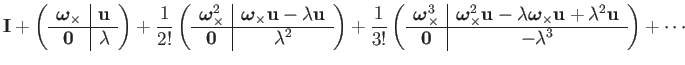 |
(147) |
The series is similar to that for
![]() , but now rotation,
translation and scale are being interleaved infinitesimally. The rotation
and scale components of the exponential are immediately clear, but
the translation component involves the mixing of the three. We can
write out the series for the translation multiplier:
, but now rotation,
translation and scale are being interleaved infinitesimally. The rotation
and scale components of the exponential are immediately clear, but
the translation component involves the mixing of the three. We can
write out the series for the translation multiplier:
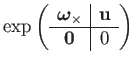 |
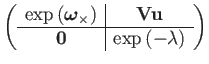 |
(148) | |
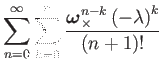 |
(149) | ||
 |
(150) | ||
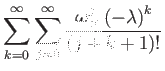 |
(151) |
Again letting
![]() ,
and using the identity from Eq. 9, we partition the
terms into odd and even powers of
,
and using the identity from Eq. 9, we partition the
terms into odd and even powers of
![]() ,
and factor:
,
and factor:
![$\displaystyle \left(\sum_{k=0}^{\infty}\dfrac{\left(-\lambda\right)^{k}}{\left(...
...2i+1}}{(2i+k+2)!}+\dfrac{\boldsymbol{\omega}_{\times}^{2i+2}}{(2i+k+3)!}\right]$](img279.png) |
(152) | ||
 |
(153) |
The first coefficient is easily identified as a Taylor series, leaving the other two coefficients to be analyzed:
Consider coefficient ![]() :
:
 |
(158) | ||
![$\displaystyle \sum_{i=0}^{\infty}\left[(-1)^{i}\theta^{2i}\sum_{k=0}^{\infty}\dfrac{\left(-\lambda\right)^{k}}{(2i+k+2)!}\right]$](img285.png) |
(159) | ||
![$\displaystyle \sum_{i=0}^{\infty}\left[\dfrac{(-1)^{i}\theta^{2i}}{\lambda^{2i}}\sum_{k=0}^{\infty}\dfrac{\left(-\lambda\right)^{2i+k}}{(2i+k+2)!}\right]$](img286.png) |
(160) | ||
![$\displaystyle \sum_{i=0}^{\infty}\left[\dfrac{(-1)^{i}\theta^{2i}}{\lambda^{2i}}\sum_{m=2i}^{\infty}\dfrac{\left(-\lambda\right)^{m}}{(m+2)!}\right]$](img287.png) |
(161) | ||
![$\displaystyle \sum_{i=0}^{\infty}\left(\dfrac{(-1)^{i}\theta^{2i}}{\lambda^{2i}...
...m+2)!}-\sum_{m=0}^{2i-1}\dfrac{\left(-\lambda\right)^{m}}{(m+2)!}\right]\right)$](img288.png) |
(162) | ||
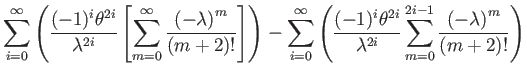 |
(163) |
Manipulating the second term yields a more useful form:
![$\displaystyle \sum_{i=0}^{\infty}\left(\dfrac{(-1)^{i}\theta^{2i}}{\lambda^{2i}}\left[\sum_{m=0}^{\infty}\dfrac{\left(-\lambda\right)^{m}}{(m+2)!}\right]\right)$](img291.png) |
(164) | ||
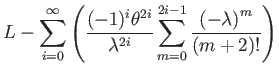 |
(165) | ||
![$\displaystyle L-\sum_{i=0}^{\infty}\left(\dfrac{(-1)^{i}\theta^{2i}}{\lambda^{2...
...ght)^{2p}}{(2p+2)!}+\dfrac{\left(-\lambda\right)^{2p+1}}{(2p+3)!}\right]\right)$](img293.png) |
(166) | ||
![$\displaystyle L-\sum_{i=0}^{\infty}\left(\dfrac{(-1)^{i}\theta^{2i}}{\lambda^{2...
...mbda\right)^{2p}\left[\dfrac{1}{(2p+2)!}-\dfrac{\lambda}{(2p+3)!}\right]\right)$](img294.png) |
(167) | ||
![$\displaystyle L-{\displaystyle \sum_{p<i}^{\infty}}\left(\dfrac{(-1)^{i}\theta^...
...mbda\right)^{2p}\left[\dfrac{1}{(2p+2)!}-\dfrac{\lambda}{(2p+3)!}\right]\right)$](img295.png) |
(168) | ||
![$\displaystyle L-{\displaystyle \sum_{p<i}^{\infty}}\left(\dfrac{(-1)^{i}\theta^...
...lambda^{2(i-p)}}\left[\dfrac{1}{(2p+2)!}-\dfrac{\lambda}{(2p+3)!}\right]\right)$](img296.png) |
(169) | ||
![$\displaystyle L-{\displaystyle \sum_{p=0}^{\infty}\sum_{q=1}^{\infty}}\left(\df...
...(2p+2)!}-\lambda\left(\dfrac{(-1)^{p}\theta^{2p}}{(2p+3)!}\right)\right]\right)$](img297.png) |
(170) | ||
![$\displaystyle L-\left(\sum_{q=1}^{\infty}\dfrac{(-1)^{q}\theta^{2q}}{\lambda^{2...
...(2p+2)!}-\lambda\left(\dfrac{(-1)^{p}\theta^{2p}}{(2p+3)!}\right)\right]\right)$](img298.png) |
(171) | ||
![\begin{displaymath}\begin{array}[t]{l}
\left(\sum_{i=0}^{\infty}\dfrac{(-1)^{i}\...
...{(-1)^{p}\theta^{2p}}{(2p+3)!}\right)\right]\right)
\end{array}\end{displaymath}](img299.png) |
(172) |
Relabel the factors:
| (173) | |||
| (174) | |||
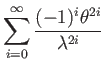 |
(175) | ||
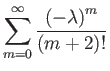 |
(176) | ||
![$\displaystyle \sum_{p=0}^{\infty}\left[\dfrac{(-1)^{p}\theta^{2p}}{(2p+2)!}-\lambda\left(\dfrac{(-1)^{p}\theta^{2p}}{(2p+3)!}\right)\right]$](img307.png) |
(177) |
The factors are then recognised as Taylor series:
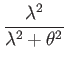 |
(178) | ||
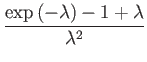 |
(179) | ||
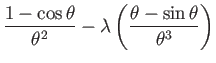 |
(180) |
By similar algebra, a formula for coefficient ![]() can be derived
from Eq. 157:
can be derived
from Eq. 157:
| (181) | |||
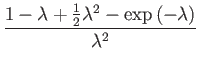 |
(182) | ||
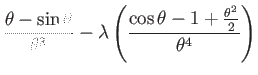 |
(183) |
Combining these results gives a closed-form exponential map for
![]() :
:
| (184) | |||
| (185) | |||
| (186) | |||
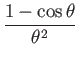 |
(187) | ||
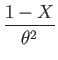 |
(188) | ||
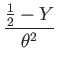 |
(189) | ||
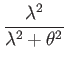 |
(190) | ||
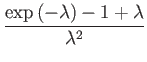 |
(191) | ||
| (192) | |||
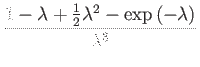 |
(193) | ||
| (194) | |||
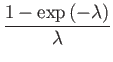 |
(195) | ||
| (196) | |||
| (197) | |||
| (198) | |||
| (199) | |||
 |
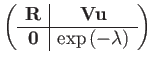 |
(200) |
Again, Taylor expansions should be used when
![]() or
or
![]() is small. The
is small. The ![]() function can be implemented by first recovering
function can be implemented by first recovering
![]() and
and ![]() , constructing
, constructing
![]() ,
and then solving for
,
and then solving for
![]() (as in the
(as in the
![]() case).
case).
Ethan Eade 2012-02-16