2.2 Exponential Map

The exponential map that takes skew symmetric matrices to rotation matrices is simply the matrix exponential over a linear combination of the generators:

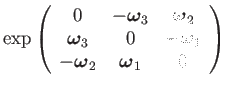$$\exp\left(\boldsymbol{\omega}_{\times}\right) \equiv \exp\left(\begin{array}{ccc} 0 & -\boldsymbol{\omega}_{3} & \bold... ...1}\\ -\boldsymbol{\omega}_{2} & \boldsymbol{\omega}_{1} & 0 \end{array}\right)$$ (6)

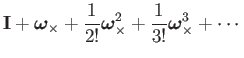$$= \mathbf{I}+\boldsymbol{\omega}_{\times}+\frac{1}{2!}\boldsymbol{\omega}_{\times}^{2}+\frac{1}{3!}\boldsymbol{\omega}_{\times}^{3}+\cdots$$ (7)

Writing the terms in pairs, we have:

$$\exp\left(\boldsymbol{\omega}_{\times}\right)=\mathbf{I}+\sum_{i=... ...s}^{2i+1}}{(2i+1)!}+\dfrac{\boldsymbol{\omega}_{\times}^{2i+2}}{(2i+2)!}\right]$$ (8)

Now we can take advantage of a property of skew-symmetric matrices:

$$\boldsymbol{\omega}_{\times}^{3}=-\left(\boldsymbol{\omega}^{T}\boldsymbol{\omega}\right)\cdot\boldsymbol{\omega}_{\times}$$ (9)

First extend this identity to the general case:

$$\theta^{2} \equiv \boldsymbol{\omega}^{T}\boldsymbol{\omega}$$ (10)

$$\boldsymbol{\omega}_{\times}^{2i+1} = (-1)^{i}\theta^{2i}\boldsymbol{\omega}_{\times}$$ (11)

$$\boldsymbol{\omega}_{\times}^{2i+2} = (-1)^{i}\theta^{2i}\boldsymbol{\omega}_{\times}^{2}$$ (12)

Now we can factor the exponential map series and recognize the Taylor expansions in the coefficients:

$$\exp\left(\boldsymbol{\omega}_{\times}\right) = \mathbf{I}+\left(\sum_{i=0}^{\infty}\dfrac{(-1)^{i}\theta^{2i}}{(... ...fty}\dfrac{(-1)^{i}\theta^{2i}}{(2i+2)!}\right)\boldsymbol{\omega}_{\times}^{2}$$ (13)

$$= \mathbf{I}+\left(1-\frac{\theta^{2}}{3!}+\frac{\theta^{4}}{5!}+\c... ...ta^{2}}{4!}+\frac{\theta^{4}}{6!}+\cdots\right)\boldsymbol{\omega}_{\times}^{2}$$ (14)

$$= \mathbf{I}+\left(\dfrac{\sin\theta}{\theta}\right)\boldsymbol{\om... ...}+\left(\dfrac{1-\cos\theta}{\theta^{2}}\right)\boldsymbol{\omega}_{\times}^{2}$$ (15)

Equation 15 is the familiar Rodrigues formula. The exponential map yields a rotation by $\theta$ radians around the axis given by $\boldsymbol{\omega}$. Practical implementation of the Rodrigues formula should use the Taylor expansions of the coefficients of the second and third terms when $\theta$ is small.

The exponential map can be inverted to give the logarithm, going from $\mathrm{SO}(3)$ to $\mathrm{so}(3)$:

$$\mathbf{R} \in \mathrm{SO}(3)$$ (16)

$$\theta = \arccos\left(\dfrac{\mathrm{tr(\mathbf{R})-1}}{2}\right)$$ (17)

$$\ln\left(\mathbf{R}\right) = \dfrac{\theta}{2\sin\theta}\cdot\left(\mathbf{R}-\mathbf{R}^{T}\right)$$ (18)

The vector $\boldsymbol{\omega}$ is then taken from the off-diagonal elements of $\ln\left(\mathbf{R}\right)$. Again, the Taylor expansion of the coefficient 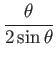$\dfrac{\theta}{2\sin\theta}$ should be used when $\theta$ is small.