Next: 2.4 Jacobians Up: 2 SO(3): Rotations in Previous: 2.2 Exponential Map
In Lie groups, it is often necessary to transform a tangent vector
from the tangent space around one element to the tangent space of
another. The adjoint performs this transformation. One very
nice property of Lie groups in general is that this transformation
is linear. For an element ![]() of a Lie group, the adjoint is written
of a Lie group, the adjoint is written
![]() :
:
| (19) | |||
| (20) |
The adjoint can be computed from the generators of the Lie algebra:
| (21) | |||
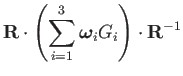 |
(22) | ||
| (23) | |||
| (24) | |||
| (25) |
In the case of
![]() , the adjoint transformation for an
element is particularly simple: it is the same rotation matrix used
to represent the element. Rotating a tangent vector by an element
``moves'' it from the tangent space on the right side of the element
to the tangent space on the left.
, the adjoint transformation for an
element is particularly simple: it is the same rotation matrix used
to represent the element. Rotating a tangent vector by an element
``moves'' it from the tangent space on the right side of the element
to the tangent space on the left.
Ethan Eade 2012-02-16