Next: 2.5 Gaussians in SO(3) Up: 2 SO(3): Rotations in Previous: 2.3 Adjoint
Consider
![]() and
and
![]() .
The rotation of vector
.
The rotation of vector
![]() by matrix
by matrix
![]() is given
by multiplication:
is given
by multiplication:
| (26) |
Then differentiation by the vector is straightforward, as ![]() is
linear in
is
linear in
![]() :
:
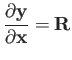 |
(27) |
Differentiation by the rotation parameters is performed by implicitly left multiplying the rotation by the exponential of a tangent vector and differentiating the resulting expression around the origin. This is equivalent to left multiplying the product by the generators.
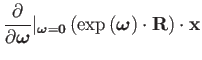 |
(28) | ||
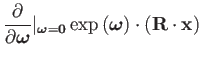 |
(29) | ||
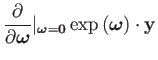 |
(30) | ||
| (31) | |||
| (32) |
Differentiation of a product of rotations is performed by the same
method. The differentation by the tangent space element
![]() is always performed around
is always performed around
![]() ,
and the adjoint is employed to shift the tangent vector left. The
result is simple:
,
and the adjoint is employed to shift the tangent vector left. The
result is simple:
| (33) | |||
![$\displaystyle \dfrac{\partial}{\partial\mathbf{\boldsymbol{\omega}}}\left[R_{1}\cdot\exp\left(\mathbf{\boldsymbol{\omega}}\right)\cdot R_{0}\right]$](img74.png) |
(34) | ||
![$\displaystyle \dfrac{\partial}{\partial\mathbf{\boldsymbol{\omega}}}\left[\exp\...
...bf{R}_{1}}\cdot\mathbf{\boldsymbol{\omega}}\right)\cdot R_{1}\cdot R_{0}\right]$](img75.png) |
(35) | ||
| (36) | |||
| (37) |
Ethan Eade 2012-02-16