Next: 3.3 Adjoint Up: 3 SE(3): Rigid transformations Previous: 3.1 Representation
The exponential map from
![]() to
to
![]() is
the matrix exponential on a linear combination of the generators:
is
the matrix exponential on a linear combination of the generators:
| (61) | |||
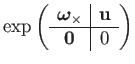 |
(62) | ||
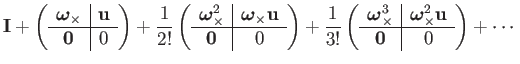 |
(63) |
The rotation block is the same as for
![]() , but the translation
component is a different power series:
, but the translation
component is a different power series:
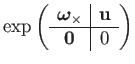 |
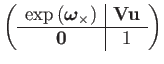 |
(64) | |
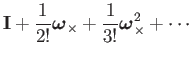 |
(65) |
Again using the identity from Eq. 9, we split the terms by odd and even powers, and factor out :
![$\displaystyle \mathbf{I}+\sum_{i=0}^{\infty}\left[\dfrac{\boldsymbol{\omega}_{\...
...s}^{2i+1}}{(2i+2)!}+\dfrac{\boldsymbol{\omega}_{\times}^{2i+2}}{(2i+3)!}\right]$](img140.png) |
(66) | ||
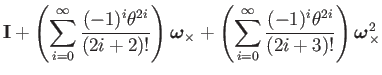 |
(67) |
The coefficients can be identified with Taylor expansions, yielding
a formula for
![]() :
:
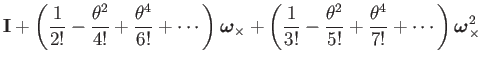 |
(68) | ||
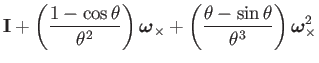 |
(69) |
Thus the exponential map has a closed-form representation:
| (70) | |||
| (71) | |||
| (72) | |||
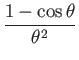 |
(73) | ||
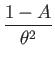 |
(74) | ||
| (75) | |||
| (76) | |||
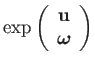 |
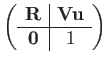 |
(77) |
For implementation purposes, Taylor expansions of ![]() ,
, ![]() , and
, and
![]() should be used when
should be used when
![]() is small.
is small.
The ![]() function on
function on
![]() can be implemented by first
finding
can be implemented by first
finding
![]() as shown in Eq. 18, then constructing
as shown in Eq. 18, then constructing
![]() , and finally solving
, and finally solving
![]() for
for
![]() (e.g. using Gaussian elimination with partial pivoting).
(e.g. using Gaussian elimination with partial pivoting).
Ethan Eade 2012-02-16